Este profesor está convencido de que para aprender matemáticas, estas deben ser manipulativas. Por esta razón, utilizó un sencillo teorema para captar la atención de sus estudiantes. Mira cómo lo hizo en este divertido y didáctico video.
Miguel Álvaro, más conocido en redes como es profesor de matemática en una escuela en España y muchos lo conocen en redes como “El profe Miguel”. Como otros docentes, Miguel intenta todos los días, en la sala de clase, cautivar a sus estudiantes con una ciencia a la que muchos niños le temen: las matemática.
Él sabe muy bien que si no se presentan de una forma innovadora, la matemática puede ser una especie de ladrillo para los estudiantes, razón por la cual decidió darle un toque bastante particular a uno de los temas que enseña: la geometría. Desde su punto de vista, la geometría es “la cenicienta del currículo de matemáticas”, pues se explica de manera axiomática y a final queda sólo como un conjunto de definiciones y fórmulas que se aplican para obtener resultados descontextualizados que se olvidan con facilidad. Él asegura que las matemática tienen que ser manipulativas, pues si éstas no se hacen con las manos, pierden todo el sentido.
Así entonces, decidió darle un poco de alegría al cálculo de áreas, ofreciéndole a los estudiantes una herramienta para contrastar resultados y llegar a estos por dos vías diferentes.
¿Cómo lo hizo? Aprovechó el Teorema de Pick para darle una nueva perspectiva al aprendizaje de la geometría. Evitando las fórmulas complejas y utilizando este modelo basado en la suma de puntos para medir áreas, Miguel logró mostrar una nueva forma de hacer las cosas. Después de eso, llevó a sus estudiantes a los pasillos del colegio para aplicar lo aprendido sobre las paredes (que parecen geoplanos). Luego los invitó a hacer un video que pusiera en evidencia el ejercicio hecho fuera del aula. ¿Y qué logró con esto? Que sus estudiantes realmente hicieran matemática con las manos y que uno de los estudiantes más inseguros (con pánico escénico al pasar a la pizarra), hiciera parte de los ejercicios y saliera como protagonista del video que crearon en grupos.

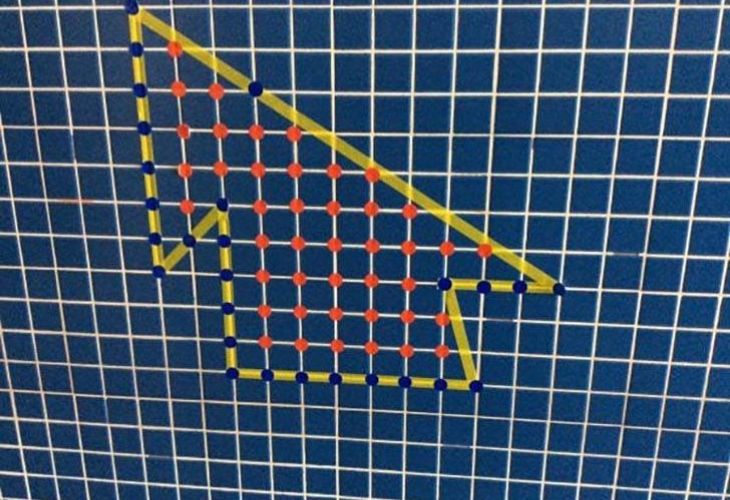
El Teorema de Pick explicado por Miguel
“El Teorema de Pick es una manera sencilla de calcular el área de un polígono simple (de una sola pieza) cuyos vértices se hallan sobre los puntos de un geoplano (una cuadrícula, como la de los cuadernos escolares).
Si llamamos D al número de puntos que quedan dentro del polígono y B al número de puntos que quedan en el borde, la fórmula de pick tiene este aspecto:

Por ejemplo, vamos a aplicar el Teorema de Pick a este polígono:
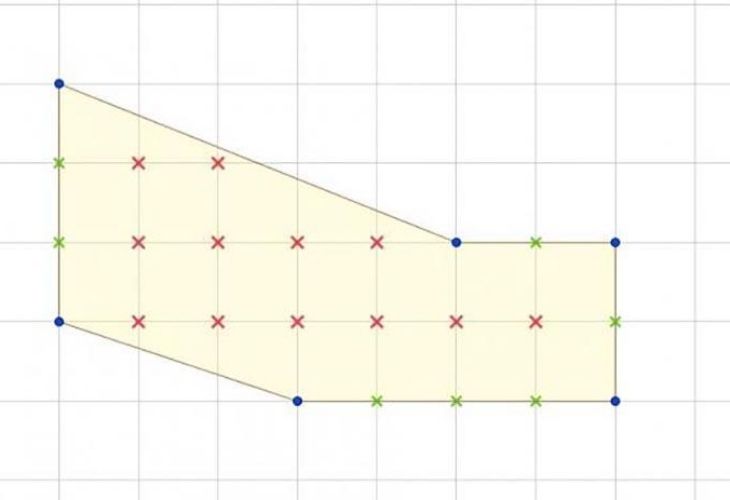
Sobre el polígono hemos marcado en azul los vértices, en rojo los puntos interiores y en verde los puntos del borde. En este caso D= 12 y B=13, por lo tanto la fórmula de Pick queda así:
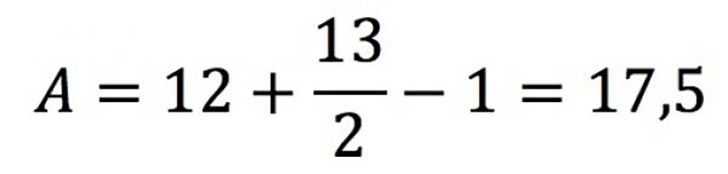
Es decir, el área de este polígono es 17,5 unidades de superficie. Podemos comprobar que el cálculo es correcto descomponiendo el área en triángulos y rectángulos, como en la imagen de aquí abajo:
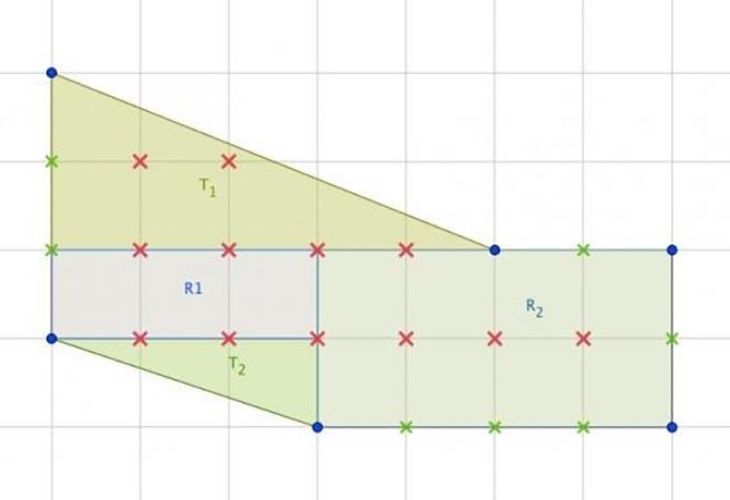






Leave a Reply Cancel reply