¿Cómo hablarle a los estudiantes de geometría desde sus propios intereses? El balón de fútbol es una de tantas alternativas. Aquí te contamos por qué.
La ciencia del balón de fútbol: una gran forma de abordar la geometría
Carlos Caszely es un periodista deportivo y exfutbolista chileno, un referente importante del club Colo Colo, una institución dedicada al fútbol profesional en la ciudad de Santiago de Chile. En un video promocional creado por la Universidad de Chile, Caszely muestra cómo un objeto geométrico, sólo con “inflarse”, puede convertirse en aquel objeto esférico que todos conocemos como balón de fútbol. Parece muy simple, pero su afirmación, hecha en un contexto de comedia, evidencia que la ciencia está en las cosas más cotidianas, incluso en el fútbol, lo que permite crear una base de contenidos divertidos e interesantes para captar la atención de los jóvenes. Pero, específicamente ¿cuál es la ciencia detrás del balón de fútbol?

Universidad de Chile
Esta es la historia…
El modelo clásico del balón de fútbol (que tiene 20 hexágonos blancos y 12 pentágonos negros), fue ideado por la marca deportiva Adidas a fines de los años 60. En ese entonces se les dio el nombre de Telstar en honor al primer satélite comercial de comunicaciones de la historia que tenía unos colores y un diseño geométrico similar. En la geometría, los Telstar son el reflejo de un objeto denominado icosaedro truncado esférico –el icosaedro es uno de los cinco poliedros regulares convexos que existen–. Este icosaedro truncado resulta del corte de las puntas de un icosaedro a lo largo de planos bien posicionados, de modo que tras el corte todas las aristas tengan la misma longitud. De aquellos cortes, surgen caras pentagonales que transforman las caras triangulares en hexagonales.
¿Por qué el balón es como es?
La geometría también explica por qué el balón tiene la forma que tiene y por qué no puede tener todas sus caras hexagonales y regulares. Cada ángulo de un hexágono regular mide 120º; al juntar tres de ellos en un vértice común formarán un ángulo total de tres veces 120º, es decir, 360º, que es un ángulo completo. Esa configuración es plana, lo que imposibilita el “cierre” del poliedro. Por eso es necesario introducir caras con ángulos menores. Esta es una de las explicaciones, pero el trabajo de otras personas permiten descifrar si existen otras formas de crear un balón, por ejemplo, Leonhard Euler (1707-1783), un matemático y físico suizo que profundizó en una teoría llamada “topología”.
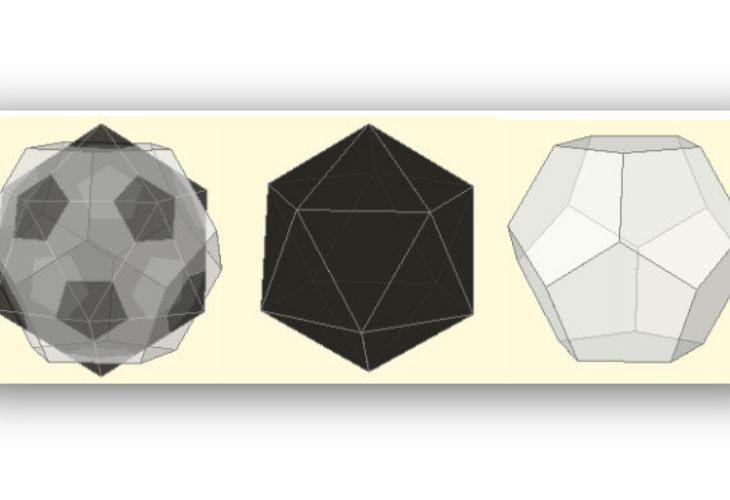
Dibujo Técnico Básico
La ciencia del balón en el aula
Toda esta explicación que parte de la historia de la pelota Telstar, hasta la justificación geométrica de la configuración de este elemento, es interesante, pues permite ver cómo un elemento tan cotidiano puede convertirse en una herramienta para abordar la historia y las ciencias exactas de una manera entretenida e interesante para la gran mayoría de estudiantes. Para científicos, matemáticos, ingenieros, arquitectos y artistas visuales, este tipo de elementos se han convertido en un puente de comunicación extraordinario, lo que demuestra que éste también puede convertirse en un puente dentro de la sala de clase.








